Hi,
here is similar example:
https://www.zacobria.com/universal-robots-knowledge-base-tech-support-forum-hints-tips/knowledge-base/script-from-host-to-robot-via-socket-connection/
V.

The Dof Community was shut down in June 2023. This is a read-only archive.
If you have questions about Robotiq products please reach our support team.
If you have questions about Robotiq products please reach our support team.
 vlastimil
vlastimil
 matthewd92
matthewd92
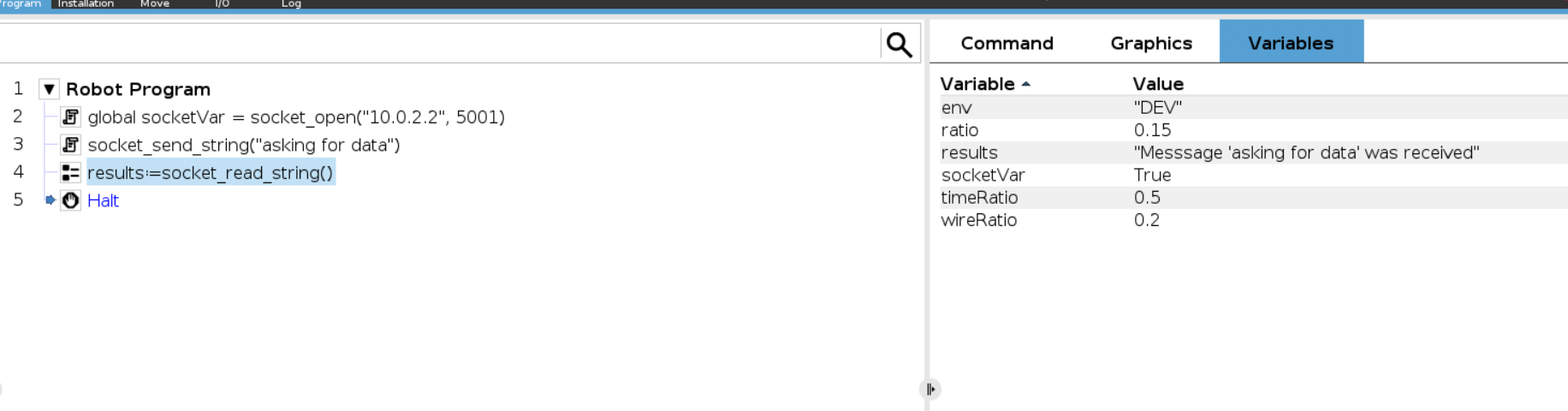
below is my simple robot program.
in sockettest v3 I get it right as shown below.
but in python I get b'asking for data'. you can see this below.
maybe not unimportantly my python code. You can see it here.