So it looks like I have a problem with calculating the intersection of the three points found by touching the surface of the blister.
The method used in the "Find Contact Offset" application does not suit for me, because I do not use the wizard. I need to calculate everything with a script, because I will find out the position in different layers of a stack of blisters.
I would like to modify the Robotiq used internal functions "relocate_orientation" or "relocate_1_touch", but I'm a bit lost in it.
In case of interest I would send how I calculate the intersection.
In case of interest I would send how I calculate the intersection.
However, the calculation is not correct, with deviations (see the pictures above).
A schematic illustration of the problem is attached:
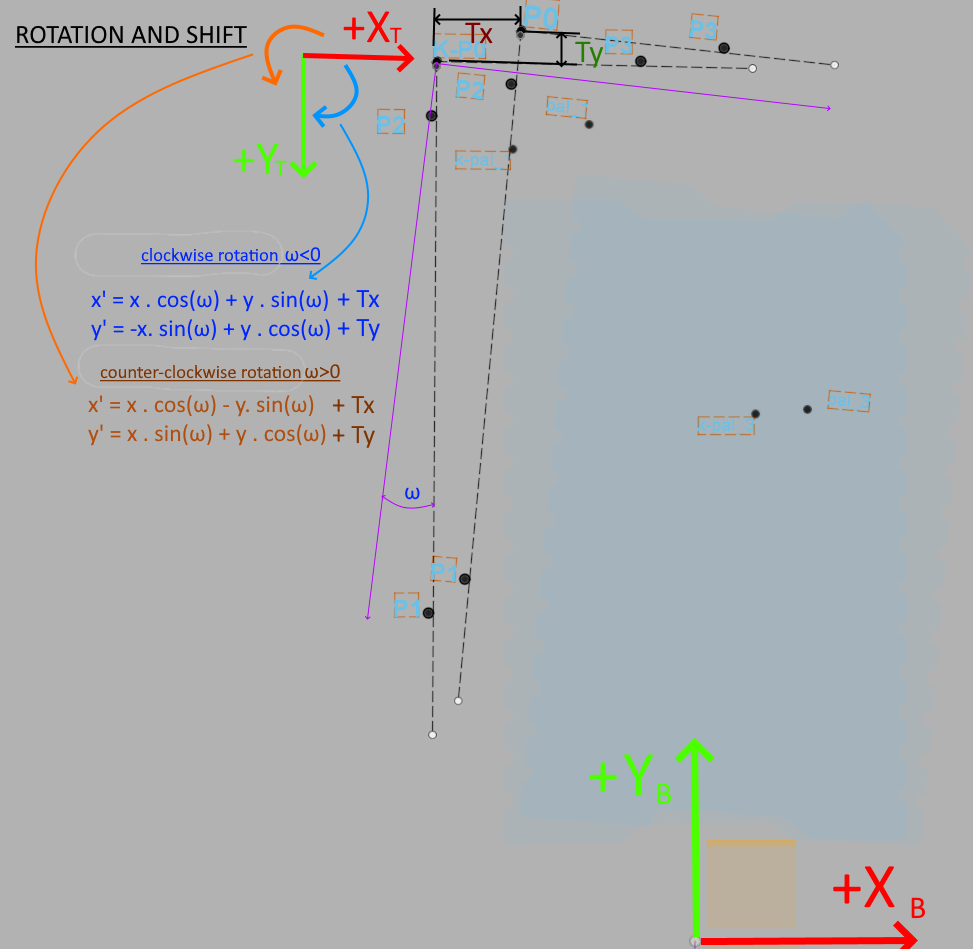
Does anyone have experience with calculating the intersection of three points (incl. rotation)?
Thanks for the advice.
Vlastimil
Vlastimil

 vlastimil
vlastimil
I have a task very similar to the example "Find Contact Offset" using #ForceCopilot.
I verified the position of the calculated by movements on this point and then by tool reference in the X and Y axes accurately copied the edges of the blister.
First, I calibrate a default position where I have teached the corner pickup points on the pallet and determine the calibration point of intersection (calibr. crosspoint K0). Then, when I rotate and move the blister, I find a new intersection of the changed position of the blister P0.
To find new corner positions of the palette on a rotated blister, I used this typical transformation:
Here is demo photo workplace:
TCP at the starting position of the first point on the palette:
TCP after transformation (see above) for the rotated and shifted palette (rotation Rz of tool is correct):
Thanks a lot for your advice.
Vlastimil